# 소방설비기사 필수 이론: 중첩의 원리, 테브낭의 정리, 노튼의 정리
소방설비기사를 준비하는 수험생 여러분, 전기 및 회로에 관련된 이론은 소방설비에서도 필수적으로 이해해야 할 부분입니다. 중첩의 원리, 테브낭의 정리, 노튼의 정리는 전기 이론의 핵심이자, 소방설비의 원활한 운영에 필수적인 개념입니다. 본 블로그 포스트에서는 이 세 가지 이론이 소방설비에서 어떻게 활용되는지를 설명합니다.
## 1. 중첩의 원리
중첩의 원리는 여러 전원(Voltage Source)과 전류원(Current Source)이 포함된 회로에서 각 소스가 개별적으로 수행하는 영향을 분석할 때 유용합니다. 각 요소별로 회로를 단순화하고, 그 결과를 겹쳐 종합하여 전체 회로의 응답을 계산할 수 있습니다.
### 공식 및 예제
중첩의 원리를 활용하기 위해서는 각 전원에 대해 회로를 해결해야 합니다. 예를 들어, 두 전압원이 있는 회로에서 한 전압원을 제거하고 나머지 전압원의 영향을 계산합니다. 그런 다음 전압원의 여러 효과를 합산하여 전체 회로에서의 각 요소의 전압과 전류를 구할 수 있습니다.
– V_total = V1′ + V2′
여기서 V1’과 V2’는 각각 각 전원에 의해 유도된 전압입니다.
### 소방설비에서의 적용
소방설비의 경보 시스템은 여러 전원 소스를 기반으로 작동하는 복잡한 회로입니다. 이러한 경우 중첩의 원리는 각 전원 소스가 경보 시스템의 다양한 부품에 어떻게 영향을 미치는지 분석할 때 유용합니다. 중첩의 원리를 통해 각 전원 소스의 개별적 영향력을 평가하고 이를 조정하여 경보의 신뢰성을 증가시킬 수 있습니다.
## 2. 테브낭의 정리
테브낭의 정리는 복잡한 회로를 단일 전압원과 저항(임피던스)의 직렬 연결로 등가화하는 방법입니다. 이는 복잡한 회로 분석을 크게 단순화할 수 있습니다.
### 공식 및 예제
테브낭 등가 회로는 다음과 같이 표현될 수 있습니다:
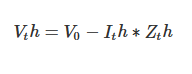
여기서 V_th는 테브낭 전압, I_th는 테브낭 정류 전류, Z_th는 테브낭 저항입니다.
### 소방설비에서의 적용
소방설비에서 구체적 예로는, 복잡한 회로 네트워크로 이루어진 화재 감지 및 방재 시스템을 들 수 있습니다. 테브낭의 정리를 통해 이러한 시스템을 간단한 등가 회로로 변환함으로써 손쉬운 분석과 문제 해결이 가능합니다. 이를 통해 유지보수 및 문제가 발생했을 때 빠른 대응이 가능해집니다.
## 3. 노튼의 정리
노튼의 정리는 테브낭의 정리와 유사하지만, 회로를 한 개의 전류원과 병렬 저항으로 변환합니다. 이는 병렬 연결의 분석에 유리합니다.
### 공식 및 예제
노튼 등가 회로는 다음과 같이 기술됩니다:
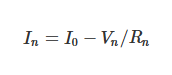
여기서 I_n는 노튼 전류, V_n는 노튼 전압, R_n는 노튼 저항입니다.
### 소방설비에서의 적용
소방회로에서 예를 들면, 노튼의 정리를 사용하여 다수의 병렬 연결된 스프링클러와 같은 장비의 전류 분배를 단순화할 수 있습니다. 이렇게 하면 전반적인 전류 분배를 이해하고 문제가 있는 스프링클러가 시스템 전체에 미치는 영향을 줄일 수 있습니다.
## 결론
중첩의 원리, 테브낭의 정리, 노튼의 정리는 소방설비와 같은 복잡한 전기 시스템에서 비효율성을 제거하고 문제 해결을 용이하게 합니다. 이러한 이론을 숙지하고 실제 상황에 적용함으로써 설비의 신뢰성과 효율성을 극대화할 수 있습니다. 독자 여러분이 이러한 이론을 토대로 소방설비기사 자격증을 준비하는 데 큰 도움이 되기를 바랍니다.