## 소방설비기사 공부를 위한 주회적분 법칙과 직선전류
소방설비기사를 준비하는 많은 수험생들은 전기 및 자성의 기본 원리를 이해하는 데 어려움을 겪곤 합니다. 특히 주회적분 법칙에 의한 계산은 소방설비의 핵심 중 하나로, 이를 완벽히 이해하는 것이 중요합니다. 오늘은 주회적분 법칙을 기반으로 한 유한장 직선전류와 무한장 직선전류의 계산에 대해 알아보겠습니다.
### 주회적분 법칙이란?
주회적분 법칙은 맥스웰 방정식 중 하나로, 공간에서 자기장을 계산하는 방법에 대해 설명합니다. 특히, 자기장과 전류 사이의 관계를 설명하는 이 법칙은 소방설비에서 자성체를 다루거나 전류에 의한 자기장을 계산할 때 매우 중요합니다. 공식은 다음과 같습니다:
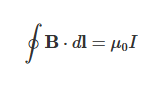
여기서 \(\mathbf{B}\)는 자기장의 벡터, \(d\mathbf{l}\)은 경로의 미소 길이, \(\mu_0\)는 자유 공간의 투자율, \(I\)는 경로를 지나는 총 전류입니다.
### 유한장 직선전류의 계산 예
유한장 직선전류는 실제 소방설비 회로에서도 자주 발생하는 상황으로, 이를 이해하는 것은 매우 중요합니다. 유한한 길이를 가진 직선 전류에 의해 생성되는 자기장은 비오-사바르 법칙을 사용하여 계산할 수 있습니다. 비오-사바르 법칙에 의한 자기장은 다음과 같습니다:
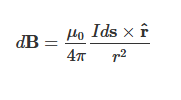
여기서 \(d\mathbf{B}\)는 미소 자기장, \(I\)는 전류, \(d\mathbf{s}\)는 전류 요소의 미소 벡터, \(\mathbf{\hat{r}}\)는 단위 위치 벡터, \(r\)은 거리입니다.
유한한 길이의 직선 전류에 의한 자기장을 구하기 위해서는 전류의 시작과 끝 점을 기준으로 적분을 수행해야 합니다. 실제 소방설비나 건물 내 배선의 자기장 계산 시에는 이 공식을 활용하여 위험 요소를 평가하게 됩니다.
### 무한장 직선전류의 자기장 계산
무한장 직선전류는 실무에서 이상적인 모형으로 간주되지만, 많은 경우에 유용한 근사치를 제공합니다. 무한히 긴 직선 전류에 의한 자기장은 주회적분 법칙을 통해 간단히 계산할 수 있습니다:
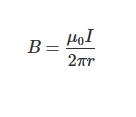
여기서 \(B\)는 직선 전류로부터 거리 \(r\) 지점에서의 자기장입니다. 이 공식은 전류의 길이가 무한히 길다는 가정 하에 적용되며, 소방 회로에서 배선이 긴 경우 이 공식을 통해 자기장 분포를 이해할 수 있습니다.
### 적용 예제: 소방설비에서의 활용
1. **화재 감지기 경로 설계**: 화재 감지기의 배선 길이가 길 경우 배선이 만드는 자기장을 고려하여 오작동을 방지해야 합니다. 유한장/무한장 직선전류 모델을 통해 전자기적 간섭을 최소화할 수 있는 경로 설계가 가능합니다.
2. **전기 화재 방지**: 전기 화재의 주요 원인 중 하나는 과부하에 의한 절연체의 손상입니다. 직선전류에 의한 자기장 계산은 전류 경로에서의 열 변화를 예측하여 예방 조치를 취하는 데 사용됩니다.
### 결론
소방설비기사를 준비하면서 주회적분 법칙을 이해하는 것은 필수적입니다. 특히 유한장 직선전류와 무한장 직선전류에 대한 계산은 복잡한 소방설비 내 전자기 환경을 이해하고 설계하는 데 큰 도움을 줍니다. 이러한 기본 원리를 확실히 이해함으로써 더 나은 설비 설계와 안전한 대처방안을 마련할 수 있습니다. 소방설비기사를 목표로 하는 수험생이라면 이와 같은 기초 공식을 확실히 이해하고 응용할 수 있어야 할 것입니다.