## 소방설비기사(전기) 주회적분 법칙과 관련 계산 예시
안녕하세요, 소방기술사입니다. 오늘은 소방설비기사(전기) 공부를 하시는 분들을 위해 주회적분 법칙에 대한 설명과 직선전류, 원형전류, 그리고 솔레노이드와 같은 다양한 전류 형태에서의 계산 예제를 다루어 보겠습니다. 이 주제는 소방설비에서 매우 중요한 부분으로, 전자기학의 기본 원리를 이해하는 데 큰 도움이 됩니다.
### 주회적분 법칙
먼저, 주회적분 법칙(Ampère’s Law)의 기본 개념부터 살펴보겠습니다. 주회적분 법칙은 닫힌 경로를 따라 자기장의 선적분이 경로 내부를 관통하는 전류의 총합과 비례한다는 법칙입니다. 수식으로는 다음과 같이 표현됩니다:
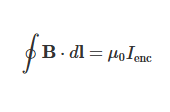
여기서:
– \(\mathbf{B}\)는 자기장(단위: 테슬라, T)
– \(d\mathbf{l}\)은 작은 경로 요소(단위: 미터, m)
– \(\mu_0\)는 자유 공간의 투자율(단위: H/m 혹은 T∙m/A), 약 \(4\pi \times 10^{-7} \text{H/m}\)
– \(I_{\text{enc}}\)는 경로 내부에 존재하는 전류(단위: 암페어, A)
### 유한장 및 무한장 직선전류
**유한장 직선전류:**
유한한 길이를 가진 직선전류에서 주회적분 법칙을 적용하기는 다소 복잡합니다. 자기장의 계산은 바이오-사바르 법칙(Biot-Savart Law)을 주로 사용합니다. 하지만 대칭이 있는 경우 주회적분 법칙을 고려해도 좋습니다.
**무한장 직선전류:**
무한장 직선전류의 경우, 전류 주위의 자기장은 원형 대칭을 가집니다. 자기장의 크기는 직선에서의 거리 \(r\)에 따라 아래와 같이 나타낼 수 있습니다:
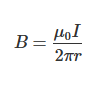
무한장 직선전류에서 주회적분 법칙을 적용하면 쉽게 자기장을 구할 수 있습니다. 예를 들어, 소방설비에서 긴 전기 배선이 있는 경우 이 공식은 주변 자기장을 예측하는 데 사용될 수 있습니다.
### 원형전류
원형전류는 전류가 원형 고리를 통해 흐를 때 마주하는 경우입니다. 중심에서의 자기장은 다음과 같이 계산됩니다:
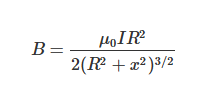
여기서:
– \(R\)은 원형 고리의 반지름(단위: m)
– \(x\)는 중심에서 떨어진 거리(단위: m)
원형전류의 경우, 중앙에서의 자기장을 측정하여 다양한 소방 감지 장비의 전자기 간섭을 최소화하는 데 사용할 수 있습니다.
### 무한장 솔레노이드
무한장 솔레노이드에서는 주회적분 법칙을 사용하여 내부의 자기장을 쉽게 계산할 수 있습니다. 솔레노이드 내부의 자기장은 균일하며, 다음과 같이 나타냅니다:
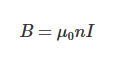
여기서:
– \(n\)은 단위 길이당 코일의 권선 수(단위: 1/m)
소방설비에서는 솔레노이드 밸브와 같은 다양한 장비가 사용되며, 이 공식은 이러한 장비의 설계 및 전자기적 특성을 이해하는 데 기여합니다.
### 환상 솔레노이드(토로이드)
환상 솔레노이드는 토로이드 형태로, 코일이 도넛 모양으로 감겨 있습니다. 주회적분 법칙에 따르면 환상 솔레노이드의 내부 자기장은 다음과 같이 나타납니다:
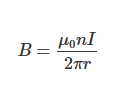
여기서:
– \(r\)은 토로이드의 중심에서의 반경(단위: m)
환상 솔레노이드는 외부 자기장 노출에 민감한 소방 장비에서 유용하며, 자기 누출이 적어 전자기 간섭을 줄일 수 있는 장점이 있습니다.
### 결론
이와 같이, 주회적분 법칙은 다양한 전류 형태에서 자기장을 이해하는 기본 원리입니다. 소방설비에서 이러한 계산법은 전자기파와 자기장의 간섭을 최소화하여 장비의 안전성과 효율성을 높이는 데 매우 중요합니다. 소방설비기사 공부를 하는 모든 분들께 이 글이 유익한 정보가 되길 바랍니다. 더불어, 실제 적용 사례와 문제 풀이를 통해 이론과 실무를 연결하는 연습을 꾸준히 하시기 바랍니다. 주회적분 법칙은 단순한 공식이 아닌, 다양한 소방 설비와의 연결고리로써 중요한 역할을 하고 있으니 꼼꼼히 이해하시길 바랍니다.
